TWiki> IVOA Web>IvoaDataModel>STC>STC-1_33-Errata>STC-1_33-Erratum-1 (2019-05-08, MarkCresitelloDittmar)
IVOA Web>IvoaDataModel>STC>STC-1_33-Errata>STC-1_33-Erratum-1 (2019-05-08, MarkCresitelloDittmar) EditAttach
EditAttach
STC-1.33 Erratum 1:
Author: DM WG Date last changed: 2019-02-04 Date accepted: 2019-04-16Rationale
This erratum is to correct an issue related to POLYGON with different orientations reported at the IVOA interop in Victoria, BC: May 2018
cite (from STC-1.33):
"The summation is over determinants of matrices formed by the position vectors xi of successive vertices; xn+1 = x1. In spherical space (left-handed coordinates) the area is:
A = - SUM[ α(i) ] – (n-2) *piαi are the polygon’s angles at the vertices. Reverse the sign for right-handed coordinates."
A = - SUM[ α(i) ] – (n-2) *piαi are the polygon’s angles at the vertices. Reverse the sign for right-handed coordinates."
Erratum Content
New Wording
- 4.5.1.4 page 30
A = + SUM[ α(i) ] – (n-2) *pi
Impact Assessment
Software using the wrong formula must be updatedExample
A = (RA,DEC)[0] = (90, 0)B = (RA,DEC)[1] = (0, 0)
C = (RA,DEC)[2] = (0, 90)
The image below shows gaphically that triangle (CCW as seen from inside the sphere, but CW as seen from outside the sphere).
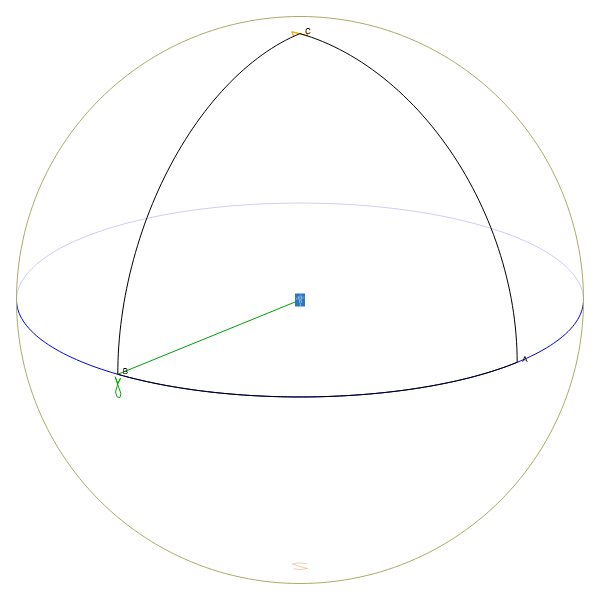 The three angles of the polygon are all 90 deg, or pi/2 rad by construction. The area is indeed: +3 * pi/2 -pi = pi/2 (1/8 of the entire sky)
The three angles of the polygon are all 90 deg, or pi/2 rad by construction. The area is indeed: +3 * pi/2 -pi = pi/2 (1/8 of the entire sky) Topic revision: r7 - 2019-05-08 - MarkCresitelloDittmar
Log in or Register
IVOA.net
Wiki Home
WebChanges
WebTopicList
WebStatistics Twiki Meta & Help
IVOA
Know
Main
Sandbox
TWiki
TWiki intro
TWiki tutorial
User registration
Notify me Working Groups Interest Groups Committees
www.ivoa.net
Documents
Events
Members
XML Schema
Wiki Home
WebChanges
WebTopicList
WebStatistics Twiki Meta & Help
IVOA
Know
Main
Sandbox
TWiki
TWiki intro
TWiki tutorial
User registration
Notify me Working Groups Interest Groups Committees
www.ivoa.net
Documents
Events
Members
XML Schema
Ideas, requests, problems regarding TWiki? Send feedback


