STC-1.33 Erratum 1:

Author: DM WG

Date last changed: 2019-02-04

Date accepted: 2019-04-16

Rationale

This erratum is to correct an issue related to POLYGON with different orientations reported at the IVOA interop in Victoria, BC: May 2018

Erratum Content

New Wording

• 4.5.1.4 page 30
  A = + SUM[ α(i) ] – (n-2) *pi

Impact Assessment

Software using the wrong formula must be updated

Example

A = (RA,DEC)[0] = (90, 0)
B = (RA,DEC)[1] = (0, 0)
C = (RA,DEC)[2] = (0, 90)
The image below shows gaphically that triangle (CCW as seen from inside the sphere, but CW as seen from outside the sphere).

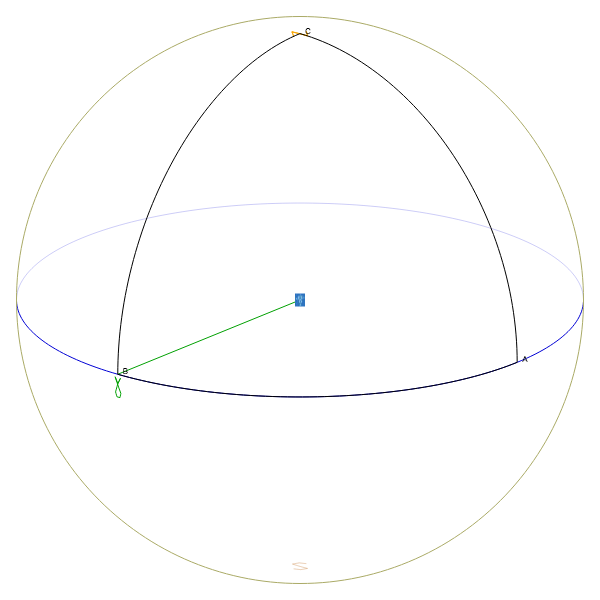The three angles of the polygon are all 90 deg, or pi/2 rad by construction. The area is indeed: +3 * pi/2 -pi = pi/2 (1/8 of the entire sky)